The most famous artefact in all Bitcoin is the white paper published by the mysterious Satoshi Nakamoto persona on October 31st, 2008. While it is beautifully written in flawless English, there are some concepts that are particularly difficult to understand. I wanted to write an article helping make its most difficult part easier to understand. This part, section 11, is the very the mathy part. It’s called “Calculations”:
Look at the snippet below. It’s got greek letters, fractions, exponents, curly brackets, the name of a French mathematician, and even computer code. But don’t worry, and don’t try to read it. I’m going to take on the challenge of explaining this and the entirety of section 11 in plain English. Let’s get started below the snippet.

You have likely heard that Satoshi solved the “double spending problem”. You may even have heard of it referred to somewhat more exotically as him having solved “The Byzantine generals’ problem”.
You may even have heard that prior to Satoshi’s solution, mathematicians had proven that the problem could not be solved. Were they wrong? Did Satoshi disprove their proof? Not exactly. What Satoshi came up with was a system that solved the problem for all practical purposes.
“Perfection is the enemy of the good” wrote the famous and witty philosopher Voltaire.
That statement captures the essence of Satoshi’s solution.
Satoshi’s solution doesn’t eliminate the possibility of a double spend, it just makes it increasingly improbable over time. In fact, it makes double spends so improbable over time that they may as well be impossible.
Let’s not get too far ahead of ourselves. A double-spend is, simply put, trying to get away with spending the same money twice. Someone who spends money shouldn’t be able to spend it again, because if they can, they either created new money out of nowhere, or the first person who thought they received the money will find out that it was actually sent to the second person it was spent to.
A good accounting system won’t let anyone get away with that.
But the challenge in Bitcoin is that there isn’t one master accountant or Chief auditor.
In Bitcoin, both you and I, and every other node operator are equals. We each account for every transaction and we each audit the whole record. But if my record shows that you sent some of your bitcoin to me, and someone else’s shows that you sent the same bitcoin to someone else, well then, we have a problem.
What’s to stop someone from sending the same bitcoins to two different people?
The first mechanism in Bitcoin that stops this is that everyone’s node — their accounting system — doesn’t allow it. If your node sees anyone attempting to spend any coins that have already been spent in the blockchain, it throws out the transaction attempting a double spend.
Well, no. There is a problem. What if someone changes the blockchain itself? The only way we all agree on what the true blockchain is by looking to see which version is the longest one. If someone could produce a longer version than the one I am holding on to, with different transactions than the one I currently have, then I’m going to throw away the old chain and replace it with the new one. And, it’s possible that this new chain might have transactions in it that send some coins to different addresses than what was reflected in the chain I held before I replaced it with this longer chain.
If someone could do this, they could ‘send’ you some bitcoin, have you perform the service you agreed to for those coins, and after that they could replace the transaction by essentially traveling backwards in time and replacing the block in which the original transaction sending coins to you was included (along with every block discovered since as well). All they have to do is produce a longer chain than the current chain replacing the block in which the original transaction was confirmed with a different block in which it isn’t present.
But doing that is not so simple. The person trying to double spend actually has to produce as many blocks as have been discovered since that original block with the transaction in it sending the coins to you. They need to produce a longer chain than the one the rest of us all have, because they need us all to throw away the currently longest chain.

And that’s very hard. And it gets harder the more blocks have been found since the original transaction was added to a block.
And this section of the white paper shows, with math, just how hard it is.
If you’re familiar with how Bitcoin works you’ll already know that to succeed with the attack described above, the attacker would need to deploy more energy than had been deployed to the whole chain since the transaction that they are seeking to undo was added to it. So if a transaction is six blocks old — roughly one hour old — then an attacker would need to deploy more energy than the entire mining network had deployed in that hour to replace the original transaction. He needs to do this before the honest network finds one more block, and that should take the whole network only ten minutes. So he’d need six to seven times as much power as the whole network to undo such a transaction. And nobody has that much equipment or access to energy.
But what if he just got lucky? Mining is, after all, a giant lottery, where miners just guess random numbers and hope that one of those will lead to the outcome of them producing a valid block. A valid block contains the fingerprints of the previous block, of all of the transactions in the current block and some metadata — and which when digested by the famous SHA256 algorithm produces a number small enough to meet the network’s requirement for validity at the time. (I’ll write a future installment explaining this if you’re not familiar with it — It’s section 4 of the white paper “Proof of Work”).
So, how lucky does an attacker have to get?
Satoshi does the math. And I’m going to put Satoshi’s math into charts.
First off, Satoshi gives an example assuming the attacker (the person trying to execute a double spend) controls 10% of the equipment and energy used to mine Bitcoin blocks at a given time. What are the odds, Satoshi asks and answers, that such an attacker might some time catch up to and overtake the current chain?
Well, that’s what all those fancy equations above show and what the code above does.
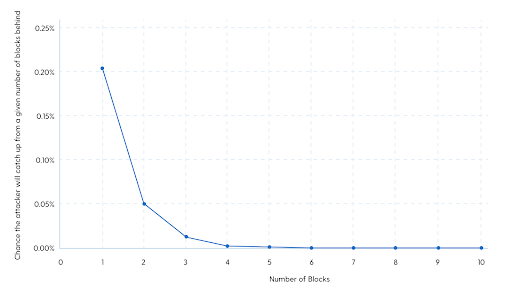
This chart shows the data in the table that Satoshi shared in the white paper. What it reveals is that if an attacker has 10% of the mining network power and tries to ‘double-spend’ a transaction from 6 blocks ago, or roughly one hour, the odds of him pulling off that attack are 0.02% or roughly 1 in 5000!
Such an attacker would have to spend all his energy and equipment not trying to mine the next block, which he has a 10% chance of succeeding at, but instead on something he only has a 1 in 5000 chance of succeeding at. So it’s 500 times harder for him to attack the network to reverse an hour old transaction than it is for him to continue strengthening the network. If he wanted to go back just 90 minutes, 9 blocks, then his chances of success 0.00046%, or worse than 1 success in 200,000 tries.
So as soon as a transaction is 6 blocks old, as long as the attacker with 10% of the network isn’t trying to reverse a transaction of more than 312 BTC, he is better off honestly mining. This is because he has a 10% chance of getting the block reward of 6.25 BTC (which is 0.625 BTC) than he is of attacking and having a 1 in 500 chance of reversing a 312 BTC transaction.
And as soon as a transaction is 9 blocks old, as long as the attacker with 10% of the network isn’t trying to reverse a transaction of more than 125,000 BTC, he is better of honestly mining than attacking.
This is what’s called assymetry.
Next, Satoshi does the same thing assuming the attacker has 30% of all the energy and equipment and goes even further back than 10 blocks — all the way to 50 blocks, or about 8 and a half hours:
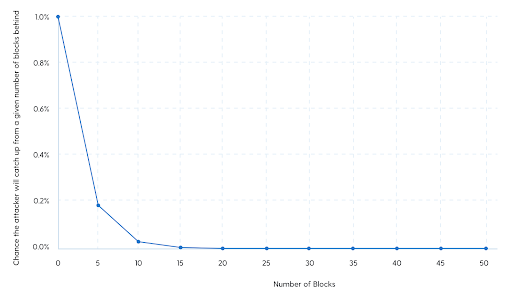
This time, the attacker has a 4% chance of being able to undo a transaction from 10 blocks prior (about 100 minutes). If they want to erase a transaction from 5 hours prior, 30 blocks, their odds of success are 0.015% or about 1 in 2000. And going back almost 7 hours, 40 blocks, is even less than a 1 in 100,000 shot.
In trying to attempt this attack, with such low odds of success, the attacker also gives up the 30% likelihood of discovering the next block and earning its reward. So this is a very expensive attack to try to pull off.
With such bad odds of attack, it is not surprising that in practice we see nobody trying to double spend.
So it’s not that Satoshi’s invention makes double spending impossible, it just makes it incredibly improbable to succeed at, and also extremely expensive to even attempt!
Finally, Satoshi provides a different way to look at these numbers and we’ll chart it below. He asks and answers, “For different levels of an attacker’s share of the mining resources, at what point does their likelihood of successfully attacking fall below 1 in 1000?” That is, how many blocks deep does a transaction have to be for an attacker with a certain percentage of the mining network to have a less than 1 in 1000 chance of undoing it if that miner chooses to attack the network instead of supporting it.
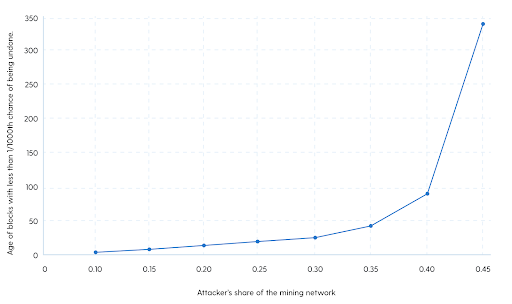
Here we see how safe Bitcoin transactions are by their age. Any attacker with 10% of the network has only a 1 in 1000 chance of erasing a transaction 5 blocks deep. In undertaking this attack they’d be giving up the 10% chance of winning the next block reward, which today is 6.25 bitcoin plus the transaction fees. That 6.25 BTC alone are worth over $250K at $40K per Bitcoin, so they’d be giving up the 10% chance of that, worth $25K, to get a 1 in 1000 chance to reverse a transaction 50 minutes old — meaning it would have to be a transaction worth 1000 times $25K or $25,000,000 for this to be a more economical, yet still improbable, gamble.
This chart also shows that even if an attacker somehow obtained 45% of the mining network’s power, they still would have only a 1 in 1000 chance of erasing transactions that are 340 blocks old, which is 56 hours, or 2.5 days. So even if such an attacker existed, the odds would be incredibly small that any transactions older than 2.5 days could be undone, and it would cost this miner 45% of the block reward each time they tried this attack, so they’d have to be trying to undo over $120 million worth of transactions to consider taking this bet.
That’s it. You now have a mathematical understanding of the difficulty of altering Bitcoin’s blockchain.
In the final analysis, Satoshi didn’t let perfection be the enemy of the good. Rather, he did do something extreme in accepting imperfection and minimizing it. His design principle can be summed in the following statement:
You don’t have to make something perfect,
And isn’t that possibly a better definition of perfect than any other you’ve ever heard?
We’ve just gone through the hardest part of the Bitcoin white paper. Part 11 — Calculations.